What are Type I and Type II Errors?
In statistical hypothesis testing, researchers use tests to make inferences about a population based on sample data. However, as with any process of decision-making, mistakes can occur. Two common types of errors in hypothesis testing are Type I and Type II errors. Understanding these errors is crucial for interpreting the results of statistical tests and ensuring that conclusions drawn from data are accurate.
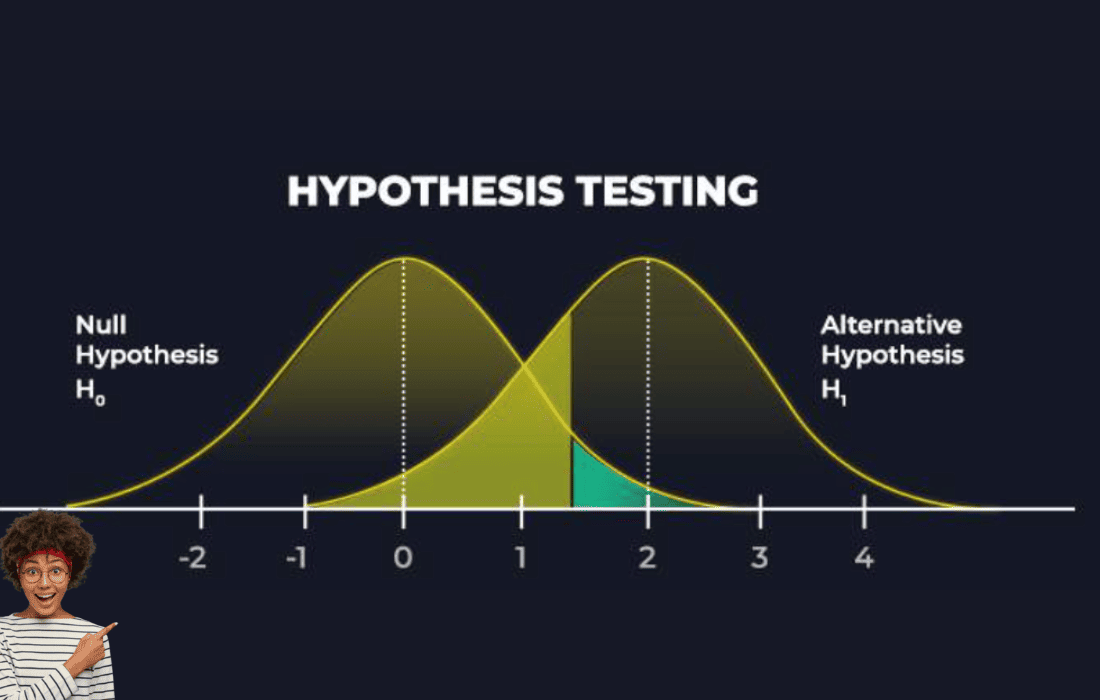
These errors arise from the misinterpretation of the relationship between the null hypothesis (H₀) and the alternative hypothesis (H₁ or Ha), which are central to hypothesis testing.
In this blog, we will explore the differences between Type I and Type II errors, their causes, and their consequences, as well as how to minimize them in statistical analysis.
The Basics of Hypothesis Testing
Before diving into the specifics of Type I and Type II errors, it’s important to understand the basics of hypothesis testing. In statistical analysis, two competing hypotheses are tested:
- Null Hypothesis (H₀): This hypothesis assumes that there is no effect or no difference in the population, and it typically represents a default or skeptical stance.
- Alternative Hypothesis (Ha or H₁): This hypothesis suggests that there is an effect, difference, or relationship in the population that is not due to chance.
The goal of hypothesis testing is to determine whether the data supports or contradicts the null hypothesis. Based on this decision, we either reject H₀ in favor of Ha (alternative hypothesis), or we fail to reject H₀ (i.e., we do not have enough evidence to support Ha).
However, the testing process is not perfect, and there are two types of errors that may occur:
Type I Error (False Positive)
A Type I error occurs when the null hypothesis (H₀) is true, but we mistakenly reject it. In other words, we incorrectly conclude that there is an effect or relationship when, in fact, there isn’t one. This error is also known as a false positive.
Explanation:
- H₀ is true (no effect or relationship exists).
- We reject H₀ and incorrectly conclude that Ha is true (an effect or relationship does exist).
- This leads to a false positive result.
Example:
Imagine a medical test designed to detect a certain disease. A Type I error would occur if the test incorrectly indicates that a healthy person (no disease) is sick, leading to a false positive diagnosis.
Significance Level (α):
The probability of committing a Type I error is denoted by α (alpha), also known as the significance level of the test. Typically, researchers set α to 0.05, meaning they are willing to accept a 5
- If α = 0.05, the test allows for a 5
Type II Error (False Negative)
A Type II error occurs when the null hypothesis (H₀) is false, but we fail to reject it. In other words, we incorrectly conclude that there is no effect or relationship when, in fact, there is one. This error is also known as a false negative.
Explanation:
- H₀ is false (an effect or relationship exists).
- We fail to reject H₀ and incorrectly conclude that there is no evidence to support Ha.
- This leads to a false negative result.
Example:
In the context of the same medical test, a Type II error would occur if the test fails to detect the disease in a person who is actually sick, leading to a false negative diagnosis.
Power of the Test (1 – β):
The probability of committing a Type II error is denoted by β (beta). The power of the test, which is the probability of correctly rejecting a false null hypothesis, is given by 1 – β.
- A higher power means a lower chance of making a Type II error. Researchers aim to maximize the power of their tests to reduce the likelihood of Type II errors.
Comparing Type I and Type II Errors
Here’s a breakdown of how Type I and Type II errors relate to the decision-making process in hypothesis testing:
| Decision | H₀ is True | H₀ is False |
|---|---|---|
| Reject H₀ (Accept Ha) | Type I Error (False Positive) | Correct Decision (True Positive) |
| Fail to Reject H₀ | Correct Decision (True Negative) | Type II Error (False Negative) |
- True Positive (TP): Correctly rejecting H₀ when it is false.
- True Negative (TN): Correctly failing to reject H₀ when it is true.
- False Positive (Type I Error): Incorrectly rejecting H₀ when it is true.
- False Negative (Type II Error): Incorrectly failing to reject H₀ when it is false.
Factors Affecting Type I and Type II Errors
Several factors influence the likelihood of making a Type I or Type II error:
- Significance Level (α): The choice of α impacts the probability of making a Type I error. A smaller α reduces the chance of Type I errors but increases the risk of Type II errors.
- Sample Size: Larger sample sizes increase the power of a statistical test, thereby reducing the risk of Type II errors. With larger samples, researchers are more likely to detect a true effect.
- Effect Size: A larger effect (or a stronger relationship between variables) makes it easier to detect the true effect, reducing the probability of a Type II error.
- Test Power: The power of a test is the probability of correctly rejecting the null hypothesis when it is false. Increasing test power reduces the risk of Type II errors.
Minimizing Type I and Type II Errors
To minimize these errors, researchers can take the following steps:
- Choose an appropriate significance level (α): Ensure that the significance level balances the risks of Type I and Type II errors. Typically, α is set at 0.05, but depending on the context, it may be adjusted.
- Increase sample size: A larger sample size increases the power of the test, reducing the chance of Type II errors.
- Use more powerful tests: Some statistical tests are more sensitive to detecting differences or effects, reducing the likelihood of Type II errors.
- Consider the consequences: In some situations, a Type I error (false positive) may have more severe consequences than a Type II error (false negative), or vice versa. It’s important to weigh the potential impacts of these errors in the context of the study.
Conclusion
Type I and Type II errors are two critical concepts in hypothesis testing. A Type I error (false positive) occurs when we incorrectly reject a true null hypothesis, while a Type II error (false negative) happens when we fail to reject a false null hypothesis. Understanding these errors helps researchers make more informed decisions about statistical tests, interpret their results with caution, and design studies that minimize the risk of making either type of error.
By carefully considering the balance between Type I and Type II errors, researchers can improve the reliability and validity of their statistical conclusions, ultimately leading to better decision-making and more accurate inferences from data.