Complete Breakdown of Machine Learning (ML)

Machine Learning

is a vast and intricate field that requires an understanding of key concepts from mathematics, statistics, programming, and data science. Let’s go through everything step-by-step, from the fundamental maths to the essential skills required to build ML models.

1. Core Concepts of Machine Learning

Machine learning revolves around creating algorithms that learn from data and make decisions based on that data. Understanding the following core areas will give you a good foundation.

• Data: ML relies heavily on data. The quality, quantity, and representation of the data play a crucial role in the performance of an ML model.
  • Training data: Used to train the model.
  • Test data: Used to evaluate the model’s performance after training.
  • Validation data: Used to tune model hyperparameters and reduce overfitting.
• Features: Variables in the data that are used as inputs to a model.
• Feature Engineering: The process of selecting and transforming raw data into features that better represent the problem you’re trying to solve.
• Labels: The target variable we want the model to predict (for supervised learning).

2. Types of Machine Learning

As we discussed earlier, ML is divided into several types:

• Supervised Learning: Learning from labeled data.
• Unsupervised Learning: Finding hidden patterns in data without labels.
• Reinforcement Learning: Learning through trial and error, receiving feedback from the environment.
• Semi-supervised Learning: A mix of labeled and unlabeled data.
• Self-supervised Learning: The system learns without explicit labels, by predicting part of the input.

3. Basic Mathematical Concepts in ML

Understanding the mathematical concepts behind ML is crucial to comprehend how algorithms work. Below are the key areas you need to understand:

3.1 Linear Algebra

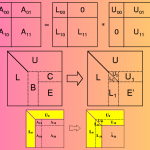
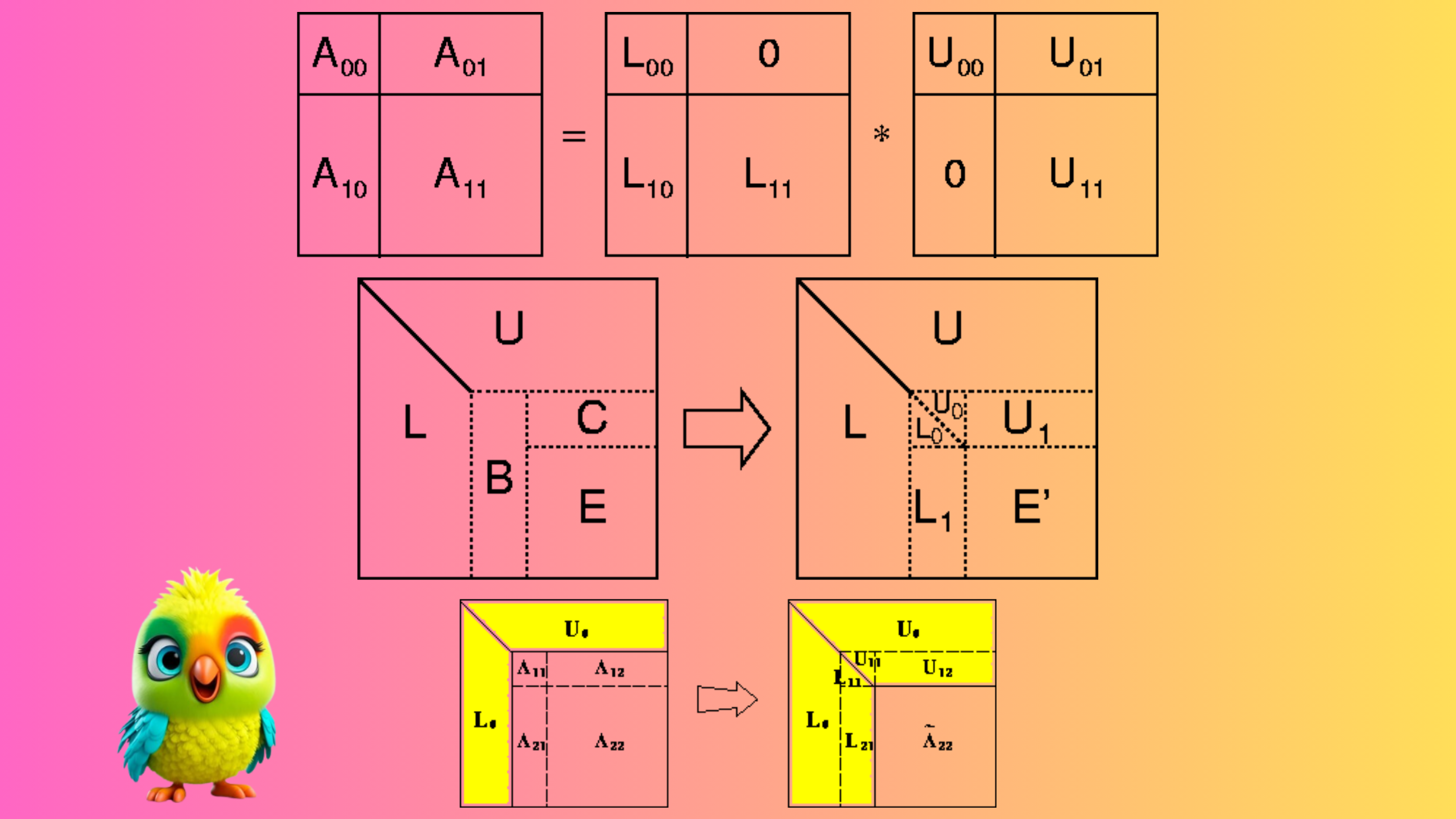
Linear algebra forms the backbone of many machine learning algorithms. It involves the study of vectors, matrices, and linear transformations.

• Scalars, Vectors, Matrices, and Tensors: Data in ML is often represented in matrices and tensors (multi-dimensional arrays). Vectors are one-dimensional arrays, matrices are two-dimensional arrays, and tensors are higher-dimensional arrays.
• Matrix Operations: Adding, subtracting, multiplying matrices (e.g., matrix-vector multiplication in neural networks).
• Dot Product: A way of multiplying vectors, used to calculate weighted sums in models like linear regression and neural networks. The dot product of two vectors v and w is given by:

• Eigenvalues and Eigenvectors: Crucial for understanding Principal Component Analysis (PCA) and many dimensionality reduction techniques. The equation A v = λ v represents an eigenvalue problem, where λ is the eigenvalue and v is the eigenvector of the matrix A.

• Singular Value Decomposition (SVD): Used in matrix factorization, often in recommendation systems. The decomposition of a matrix A into three matrices U, Σ, and V^T is written as:

3.2 Probability and Statistics

Probability theory provides the foundation for understanding how ML algorithms make predictions based on data.

• Probability Distributions: Understanding how data is distributed is essential for modeling uncertainty in ML. For example, the Gaussian (normal) distribution is given by:

where μ is the mean and σ² is the variance.

• Bayesian Inference: A way of updating probabilities based on new evidence or data. Bayes’ theorem is given by:

where P(C|X) is the posterior probability, P(X|C) is the likelihood, P(C) is the prior, and P(X) is the evidence.

3.3 Calculus

Calculus, specifically differentiation, is essential in understanding how machine learning algorithms learn by minimizing or maximizing certain functions, like cost functions or loss functions.

• Derivatives: Used in optimization algorithms like Gradient Descent, which is used to minimize the error (or loss) in a model. The derivative of a function f(x) is written as:

• Gradient: A vector of partial derivatives, representing the slope of a function in multiple dimensions. The gradient of a function f is written as:

• Gradient Descent: An optimization algorithm that updates parameters in the direction of the negative gradient of the loss function. The update rule for gradient descent is:

where θ is the parameter, η is the learning rate, and J(θ) is the cost function.

3.4 Optimization

Optimization is a mathematical process used to minimize or maximize certain functions, such as cost functions.

• Cost Function (Loss Function): A function that measures how well a model’s predictions align with the true values.
• Mean Squared Error (MSE): Commonly used in regression problems:

• Cross-Entropy Loss: Used in classification problems, especially with neural networks.

4. Key Algorithms and Models in ML

Machine learning models are based on mathematical algorithms. Here’s an overview of common ML algorithms, along with the maths behind them.

4.1 Supervised Learning Algorithms

• Linear Regression:Math: Linear regression uses the equation of a line:

It minimizes the sum of squared errors (SSE) between predicted and actual values using gradient descent.

• Logistic Regression:Math: Logistic regression uses the sigmoid function (logistic function) to predict probabilities:

where z = w⋅x + b is the weighted sum of inputs.

• Decision Trees:Math: Decision trees split the data based on the best feature that minimizes impurity (e.g., Gini Index, Entropy).

  Formula for Gini Index:

where p_i is the probability of class i in the dataset.

• Support Vector Machines (SVM):Math: SVM uses the kernel trick to find a hyperplane that maximizes the margin between classes.

where w is the weight vector, x is the input, and b is the bias term.

• K-Nearest Neighbors (k-NN):Math: The k-NN algorithm measures the distance between points (typically using Euclidean distance) and classifies data based on the majority vote of neighbors.

• Naive Bayes:Math: Naive Bayes is based on Bayes’ Theorem:

5. Practical Requirements for Machine Learning

To build effective machine learning models, you need both theoretical and practical knowledge.

• Programming Skills:
  • Python: The most widely used programming language for ML, with libraries like NumPy, Pandas, Matplotlib, Scikit-learn, TensorFlow, and PyTorch.
  • R: Another popular language for statistical analysis and data science.
• Tools and Libraries:
  • Scikit-learn: A Python library for classical machine learning algorithms (e.g., linear regression, SVM, decision trees).
  • TensorFlow/PyTorch: Deep learning libraries for building neural networks.
  • Keras: A high-level neural network API that runs on top of TensorFlow.
  • Matplotlib/Seaborn: Libraries for visualizing data and model results.
• Data Preprocessing:
  • Handling missing values, normalization/standardization, encoding categorical features, splitting data into training and test sets.
• Model Evaluation:
  • Cross-validation: Techniques like k-fold cross-validation for assessing model performance.
  • Performance Metrics: Accuracy, precision, recall, F1-score, ROC curve, AUC, etc.

Conclusion

Machine learning is an interdisciplinary field requiring strong knowledge in mathematics, programming, statistics, and domain knowledge. The foundational math skills you need to understand are linear algebra, calculus, probability, and statistics. From there, you can dive deeper into specific ML algorithms and frameworks. Additionally, a strong grasp of model evaluation, data preprocessing, and software tools will enable you to effectively apply ML techniques to solve real-world problems.