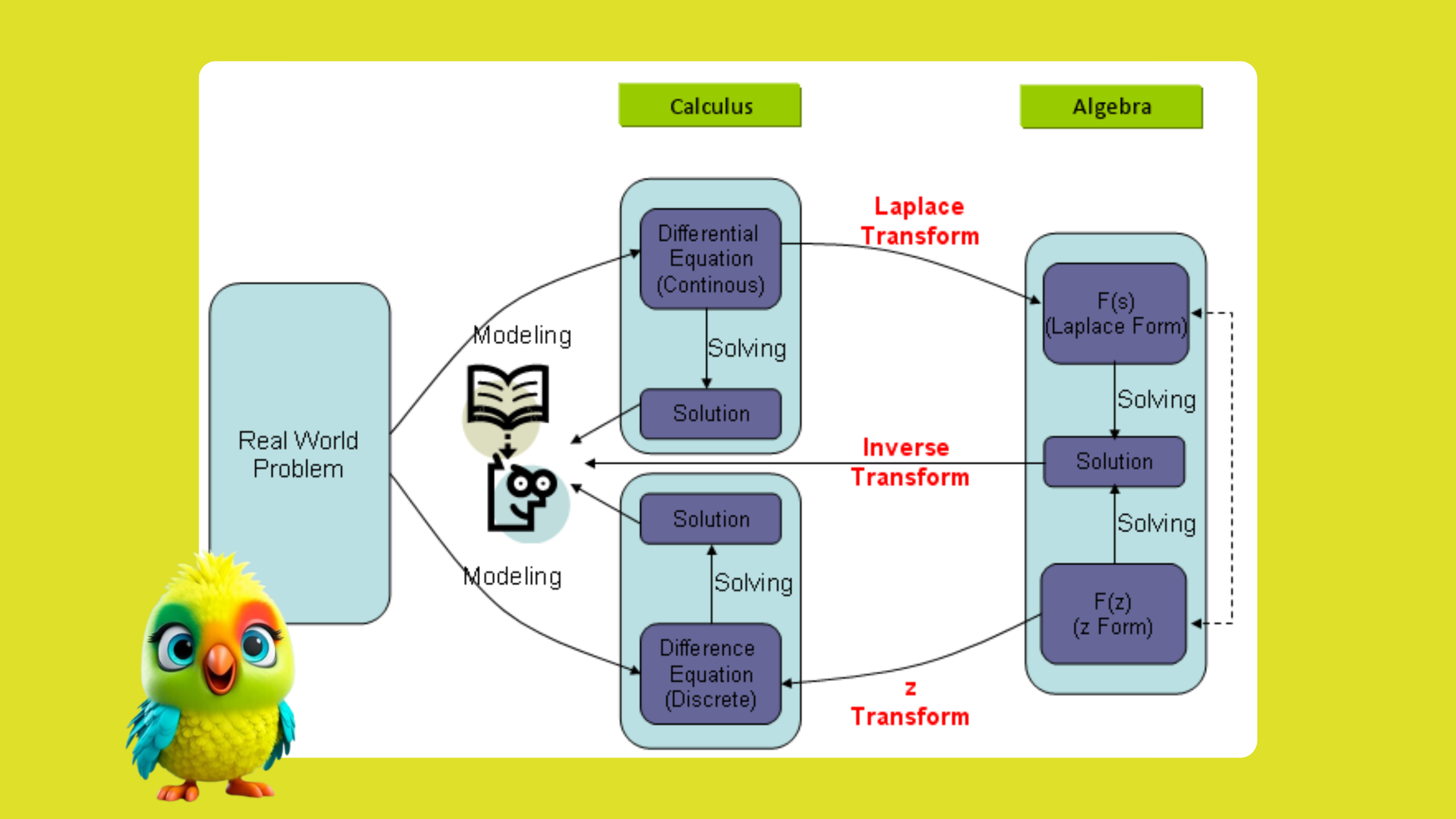
First-order ordinary differential equations (ODEs) are among the simplest types of differential equations used in mathematics and applied sciences. In this blog, we will explore the definition, classification, solution methods, and applications of first-order ODEs, breaking down the concepts for a better understanding.
What is a First-Order Ordinary Differential Equation?
A first-order ordinary differential equation is an equation that contains a function \(y(t)\) and its first derivative \(\frac{dy}{dt}\). The general form of a first-order ODE can be expressed as:
\frac{dy}{dt} = f(t, y)
\]
Where:
– \(t\) is the independent variable (typically representing time).
– \(y(t)\) is the dependent variable.
– \(f(t, y)\) is a given function of \(t\) and \(y\).
Classification of First-Order ODEs
First-order ODEs can be classified into several types based on their characteristics. The main classifications include:
1. Separable Equations
A first-order ODE is called separable if it can be expressed in the form:
\frac{dy}{dt} = g(t) h(y)
\]
This allows for separation of variables:
\frac{1}{h(y)} dy = g(t) dt
\]
2. Linear Equations
A first-order ODE is linear if it can be expressed in the standard form:
\frac{dy}{dt} + p(t) y = g(t)
\]
Where \(p(t)\) and \(g(t)\) are functions of \(t\).
3. Exact Equations
A first-order ODE is exact if it can be expressed in the form:
M(t, y) dt + N(t, y) dy = 0
\]
Where \(\frac{\partial M}{\partial y} = \frac{\partial N}{\partial t}\).
Solution Methods for First-Order ODEs
The method used to solve a first-order ODE depends on its classification:
1. Separable Equations
To solve a separable equation, we integrate both sides:
\int \frac{1}{h(y)} dy = \int g(t) dt
\]
After integration, we can solve for \(y(t)\).
2. Linear Equations
To solve a linear first-order ODE, we can use an integrating factor \(\mu(t)\):
\mu(t) = e^{\int p(t) dt}
\]
Multiplying the entire equation by the integrating factor gives:
\mu(t) \frac{dy}{dt} + \mu(t) p(t) y = \mu(t) g(t)
\]
This can be expressed as:
\frac{d}{dt}[\mu(t) y] = \mu(t) g(t)
\]
We then integrate both sides to find \(y(t)\).
3. Exact Equations
To solve an exact ODE, we find a function \(\psi(t, y)\) such that:
\frac{\partial \psi}{\partial t} = M(t, y) \quad \text{and} \quad \frac{\partial \psi}{\partial y} = N(t, y)
\]
Once \(\psi(t, y) = C\) (where \(C\) is a constant) is determined, we can express the solution.
Example: Solving a Separable First-Order ODE
Consider the equation:
\frac{dy}{dt} = k y
\]
Where \(k\) is a constant. This equation is separable since we can write it as:
\frac{1}{y} dy = k dt
\]
Integrating both sides yields:
\ln |y| = kt + C
\]
Exponentiating gives the general solution:
y(t) = C e^{kt}
\]
Where \(C\) is the constant of integration.
Applications of First-Order ODEs
First-order ordinary differential equations have numerous applications in various fields:
– Physics: Modeling population growth, radioactive decay, and cooling processes.
– Biology: Describing the growth of bacteria in cultures or the spread of diseases.
– Economics: Analyzing continuously compounded interest and investment growth.
– Engineering: Solving circuits, fluid flow, and mechanics problems.
Conclusion
Understanding first-order ordinary differential equations provides a foundation for analyzing dynamic systems in mathematics and the real world. By mastering the various methods for solving these equations, you can tackle more complex problems across different fields of study.
Further Resources
For those looking to deepen their understanding:
– Books: *Elementary Differential Equations and Boundary Value Problems* by William E. Boyce and Richard C. DiPrima.
– Online Courses: Websites like Khan Academy, Coursera, and edX provide valuable resources on differential equations.
– Software Tools: Explore MATLAB or Mathematica for hands-on experience with solving ODEs.
Happy learning, and may your journey into the world of differential equations be enlightening and rewarding!