The Mathematical Derivation of Pythagoras’ Theorem

December 2024
M	T	W	T	F	S	S
	1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30	31

Pythagoras’ Theorem is a cornerstone of mathematics, particularly in geometry. It provides a relationship between the sides of a right triangle, stating that the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides. In mathematical terms, if ( c ) is the length of the hypotenuse and ( a ) and ( b ) are the lengths of the other two sides, the theorem can be expressed as:

Remark 1. If triangle ABC is a right triangle with ( C ) as the right angle, then the following relationship holds:

The square of the length of the hypotenuse ( c ) is equal to the sum of the squares of the lengths of the other two sides ( a ) and ( b ): \begin{equation} c^2 = a^2 + b^2 \end{equation}

In this blog, we will delve into the mathematical derivation of this theorem through various approaches, including visual representations and algebraic formulations.

Understanding Pythagoras’ Theorem

Before we get into the derivation, let’s clarify what we mean by a right triangle. A right triangle is defined as a triangle that has one angle measuring ( 90^\circ ). The side opposite this angle is known as the hypotenuse, while the other two sides are referred to as the legs of the triangle.

Step 1: Setting Up the Problem

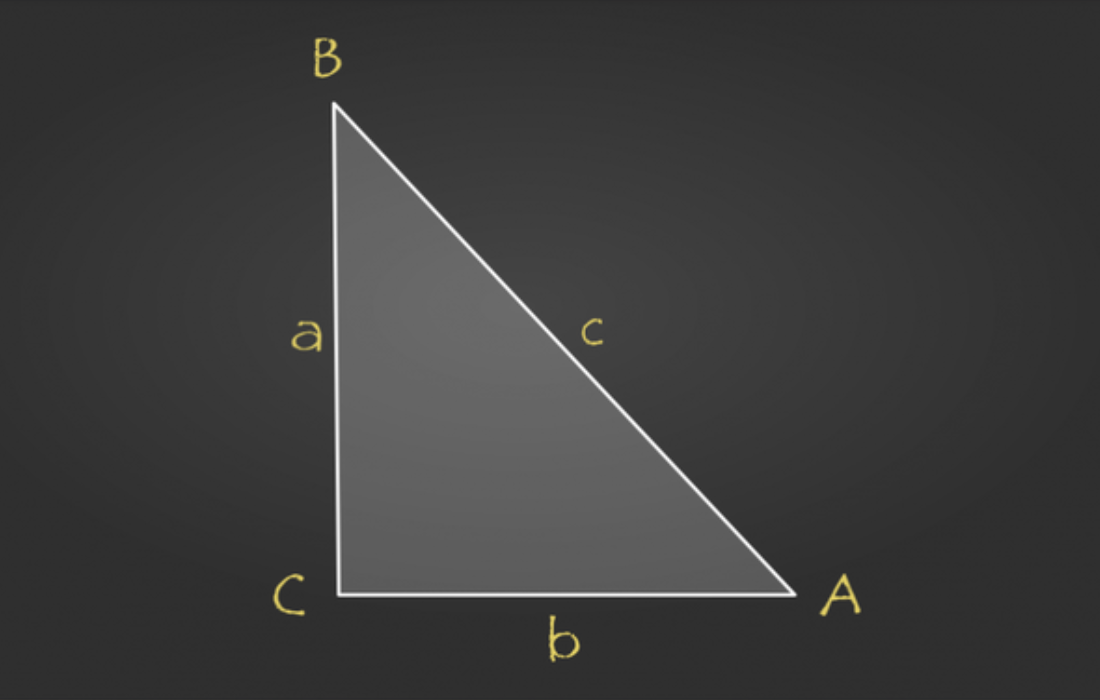
Assume we have a right triangle ( ABC ) where:

( C ) is the right angle,
( AB = c ) (the hypotenuse),
( AC = b ),
( BC = a ).

To visualize this, we can represent the triangle in the coordinate plane:

   A (0,b)
   |
   |
   |\
   | \
   |  \  c
   |   \
   |    \
   |     \
   B------C (a,0)

Step 2: Visual Approach Using Squares

Now, if we want to provide a geometric proof of the theorem, we can do so by constructing squares on each of the sides.

Construct a square with side length ( c ) on the hypotenuse ( AB ).
Construct squares on the two legs:
- A square with side length ( a ) on base ( BC ),
- A square with side length ( b ) on height ( AC ).

Visually, we now have:

Area of square on hypotenuse: ( c^2 )
Area of square on side ( a ): ( a^2 )
Area of square on side ( b ): ( b^2 )

Step 3: Analyzing Areas

The key part of the derivation involves showing that the area of the square on the hypotenuse equals the sum of the areas of the squares on the other two sides:

Remark 2. The areas satisfy the equation: \begin{equation} c^2 = a^2 + b^2 \end{equation}

To prove this, we can rearrange our geometric layout or utilize algebraic manipulation.

Step 4: Algebraic Manipulation

Let’s prove this algebraically using the distance formula in the Cartesian plane.

Set point ( C ) at the origin ( (0, 0) ).
Set point ( A ) at ( (0, b) ) and point ( B ) at ( (a, 0) ).

The distance ( c ) (the hypotenuse) can be computed using the distance formula:

Remark 3. The distance ( c ) can be expressed as: \begin{equation} c = \sqrt{(a – 0)^2 + (0 – b)^2} \end{equation}

Calculating this step by step yields:

Remark 4. After simplifying the expression, we find: \begin{equation} c = \sqrt{a^2 + b^2} \end{equation}

By squaring both sides, we derive:

Remark 5. Thus, we conclude that: \begin{equation} c^2 = a^2 + b^2 \end{equation}

This confirms the theorem.

Conclusion

Through geometric visualization and algebraic analysis, we arrive at the conclusion that Pythagoras’ Theorem ( c^2 = a^2 + b^2 ) holds true in all right triangles. Its implications stretch far beyond simple geometry, forming the basis for further concepts in mathematics, physics, and engineering.