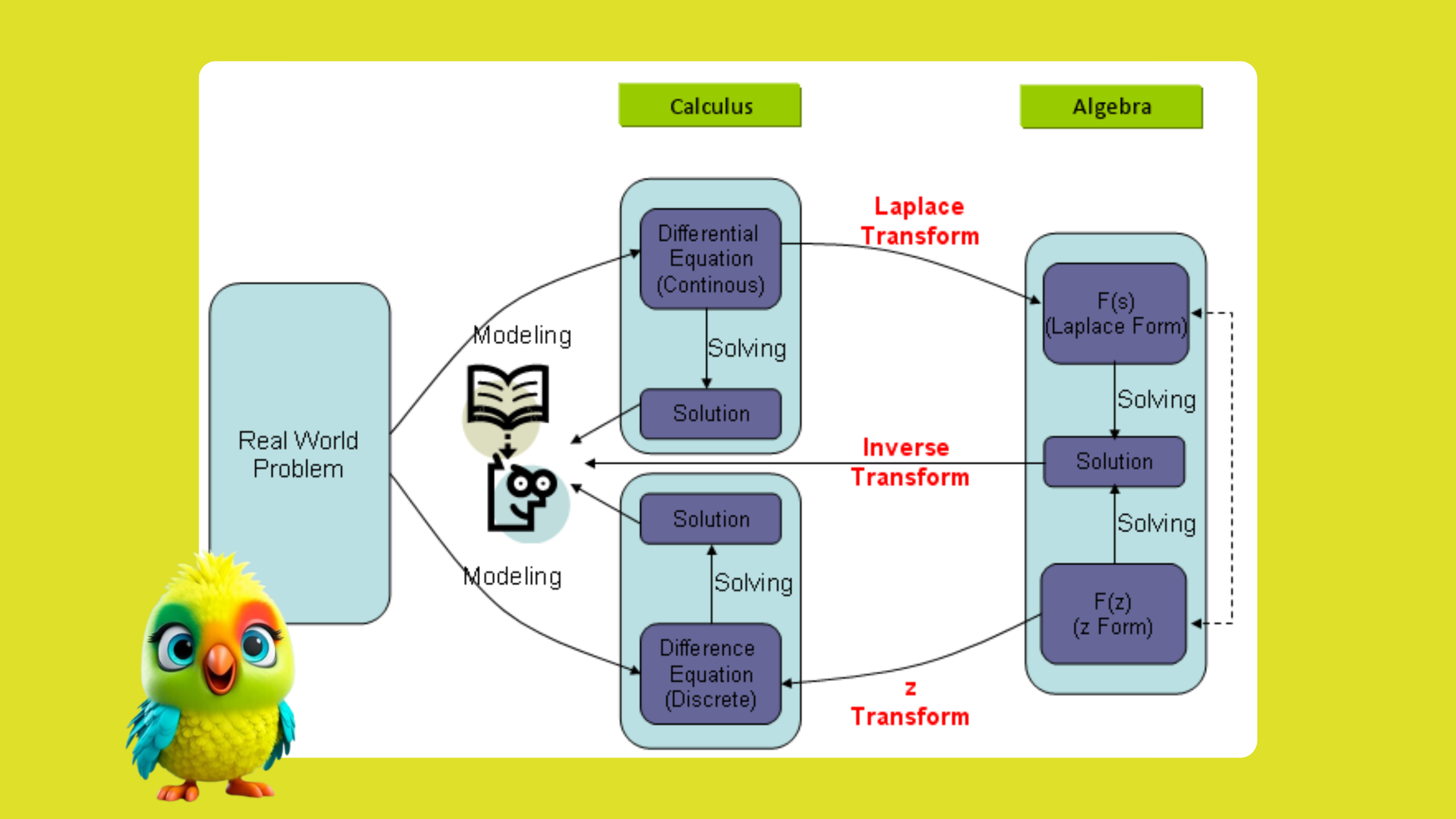
Abstract: Differential equations are fundamental in mathematics, physics, and engineering, as they describe how quantities change over time. One powerful method for solving ordinary differential equations (ODEs) is the Laplace transform. This blog will introduce the Laplace transform and demonstrate its application in solving a simple first-order ODE with a detailed example.
Table of Contents
1. What is the Laplace Transform?
2. Properties of the Laplace Transform
3. Example: Solving a First-Order ODE
1. Step 1: Take the Laplace Transform
2. Step 2: Solve for \( Y(s) \)
3. Step 3: Partial Fraction Decomposition
4. Step 4: Take the Inverse Laplace Transform
4. Verifying the Solution
5. Conclusion
6. Further Resources
1. What is the Laplace Transform?
The Laplace transform is an integral transform that converts a function of time \( f(t) \) into a function of a complex variable \( s \). It is defined as follows:
\[
\mathcal{L}\{f(t)\} = F(s) = \int_{0}^{\infty} e^{-st} f(t) \, dt
\]
Where:
– \( \mathcal{L} \) denotes the Laplace transform,
– \( f(t) \) is the original function (typically a time-domain function),
– \( F(s) \) is the transformed function (in the frequency domain).
2. Properties of the Laplace Transform
1. Linearity:
\[
\mathcal{L}\{af(t) + bg(t)\} = aF(s) + bG(s)
\]
for constants \( a \) and \( b \).
2. Differentiation:
\[
\mathcal{L}\left\{ \frac{d}{dt} f(t) \right\} = sF(s) – f(0^+)
\]
3. Integration:
\[
\mathcal{L}\left\{ \int_{0}^{t} f(\tau) \, d\tau \right\} = \frac{F(s)}{s}
\]
3. Example: Solving a First-Order ODE
Let’s solve the first-order linear ordinary differential equation:
\[
\frac{dy}{dt} + 3y = 6, \quad y(0) = 2
\]
3.1. Step 1: Take the Laplace Transform
First, we apply the Laplace transform to both sides of the equation. Recall the properties, especially the differentiation property.
Taking the Laplace transform gives us:
\[
\mathcal{L}\left\{\frac{dy}{dt}\right\} + 3\mathcal{L}\{y\} = \mathcal{L}\{6\}
\]
Using the differentiation property and the fact that the Laplace transform of a constant \( k \) is \( \frac{k}{s} \):
\[
sY(s) – y(0) + 3Y(s) = \frac{6}{s}
\]
Substituting \( y(0) = 2 \):
\[
sY(s) – 2 + 3Y(s) = \frac{6}{s}
\]
Now, we can rewrite this to isolate \( Y(s) \):
\[
sY(s) + 3Y(s) = \frac{6}{s} + 2
\]
Combining the terms gives:
\[
Y(s)(s + 3) = \frac{6 + 2s}{s}
\]
3.2. Step 2: Solve for \( Y(s) \)
Now we can solve for \( Y(s) \):
\[
Y(s) = \frac{6 + 2s}{s(s + 3)}
\]
3.3. Step 3: Partial Fraction Decomposition
Next, we perform partial fraction decomposition:
\[
Y(s) = \frac{A}{s} + \frac{B}{s + 3}
\]
Multiplying through by \( s(s + 3) \) gives:
\[
6 + 2s = A(s + 3) + Bs
\]
To find constants \( A \) and \( B \), we can set \( s = 0 \):
\[
6 = 3A \implies A = 2
\]
Now set \( s = -3 \):
\[
6 – 6 = -3B \implies B = 0
\]
Thus:
\[
Y(s) = \frac{2}{s}
\]
3.4. Step 4: Take the Inverse Laplace Transform
Now, we take the inverse Laplace transform of \( Y(s) \):
\[
y(t) = \mathcal{L}^{-1}\{Y(s)\} = \mathcal{L}^{-1}\left\{\frac{2}{s}\right\}
\]
The inverse Laplace transform of \( \frac{1}{s} \) is \( 1 \), thus:
\[
y(t) = 2
\]
4. Verifying the Solution
Now we substitute back into the original equation to verify that it holds true:
\[
\frac{dy}{dt} = 0, \quad 3y = 3(2) = 6 \quad \Rightarrow \quad 0 + 6 = 6 \quad \text{(True)}
\]
5. Conclusion
We successfully solved the first-order linear differential equation using the Laplace transform. The final solution is:
\[
y(t) = 2
\]
This powerful method can be applied to a wide variety of linear ODEs and is particularly useful for equations with initial value problems. Understanding the Laplace transform provides you with an invaluable tool in solving differential equations effectively.
6. Further Resources
1. Books:
– “Advanced Engineering Mathematics” by Erwin Kreyszig
– “Differential Equations with Applications and Historical Notes” by George F. Simmons
2. Online Courses:
– MIT OpenCourseWare – Differential Equations
– Khan Academy – Differential Equations
3. Interactive Tools:
– Wolfram Alpha (https://www.wolframalpha.com/) for solving ODEs
4. YouTube Channels:
– Mathologer
– 3Blue1Brown – particularly for intuitive understanding of math concepts