Education
Expand Your Knowledge with Our Education Courses: Learn, Grow, and Succeed
Discover a wide array of education-focused courses designed to enhance your academic and professional growth. From early childhood education to advanced teaching techniques, our courses cater to educators, parents, and anyone passionate about learning. Gain valuable skills in curriculum development, classroom management, educational technology, and more. Whether you’re looking to become a teacher, advance your career in education, or simply deepen your understanding, our courses offer the tools you need to succeed and inspire others.
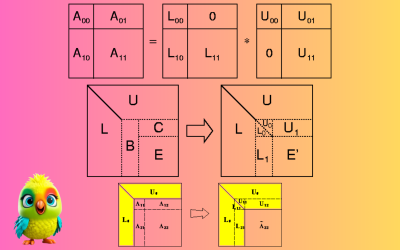
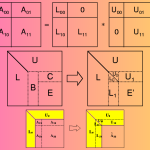
LU Decomposition Method Is A Quick, Easy, and Credible Way to Solve problem in Linear Equations
Introduction Solving systems of linear equations is a fundamental problem in mathematics, engineering, physics, and computer science. Among the various methods available, LU Decomposition stands out for its efficiency, simplicity, and numerical stability. In this blog, we’ll explore what LU Decomposition is, how it works, and why it’s a reliable method for solving linear equations. What…
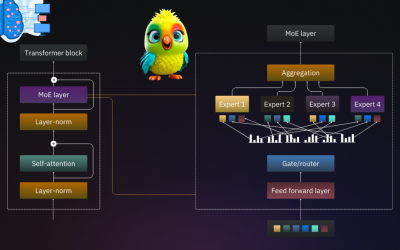
MoE Explained and visualized The Architecture Behind Efficient Large Language Models
What is Mixture of Experts? Mixture of Experts (MoE) is a technique that uses many different sub-models (or “experts”) to improve the quality of LLMs. Two main components define a MoE: Experts – Each FFNN layer now has a set of “experts” of which a subset can be chosen. These “experts” are typically FFNNs themselves. Router or gate…
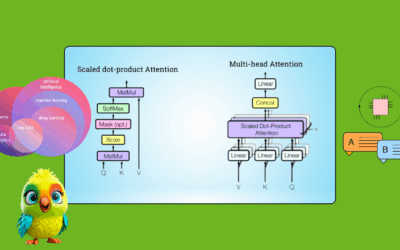
Understanding Transformers: The Mathematical Foundations of Large Language Models
In recent years, two major breakthroughs have revolutionized the field of Large Language Models (LLMs): 1. 2017: The publication of Google’s seminal paper, (https://arxiv.org/abs/1706.03762) by Vaswani et al., which introduced the Transformer architecture – a neural network that fundamentally changed Natural Language Processing (NLP). 2. 2022: The launch of ChatGPT by OpenAI, a transformer-based chatbot…
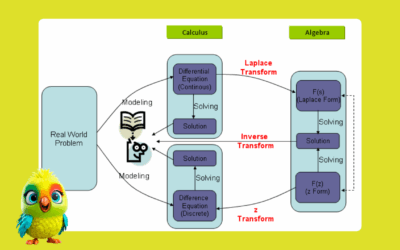
Mastering Laplace Equations and Transforms The History, Derivations, and Solved Examples
Brief Historical Introduction to Laplace Transform The Laplace Transform is a cornerstone of mathematical physics and engineering, with deep historical roots dating back to the 18th century. Named after Pierre-Simon Laplace (1749–1827), a French mathematician and astronomer, this transformative tool emerged as part of his work on probability and celestial mechanics. Origins Laplace originally used…
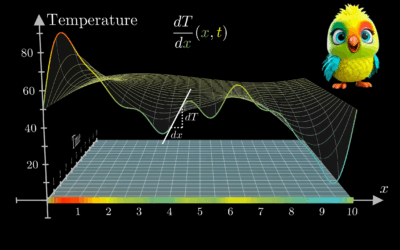
Partial Differential Equations (PDEs), Their Canonical Forms wave, heat, and Laplace equations
Partial differential equations (PDEs) are classified into different types based on their characteristics, which determine the nature of their solutions and the appropriate solution methods. The three most important PDEs in mathematical physics are: Partial differential equations (PDEs) are used in machine learning (ML)—especially in advanced fields like: Physics-informed neural networks (PINNs): These use PDEs…
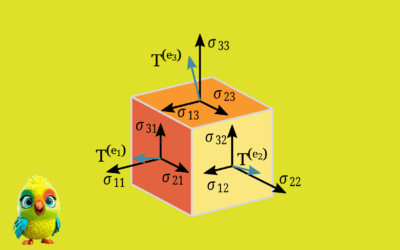
Understanding Tensors: A Comprehensive Guide with Mathematical Examples
Welcome to our mathematically rigorous exploration of tensors. This guide provides precise definitions, theoretical foundations, and worked examples ranging from elementary to advanced levels. All concepts are presented using proper mathematical notation with no reliance on programming languages. The Story of Tensors: From Curved Surfaces to Cosmic Equations Long ago, in the 19th century, a…
The Epic Saga of the Cubic Equation: From Blood Feuds to Modern Algebra
The Drama of the Cubic Equation: Rivalries, Betrayals, and Renaissance Mathematics The 16th century was a time of mathematical duels, secret solutions, and bitter rivalries. The quest to solve the cubic equation wasn’t just about algebra—it was about fame, survival, and revenge. 1. Tartaglia: The Stuttering Genius Who Outsmarted His Rivals Niccolò Tartaglia (1500–1557) was…
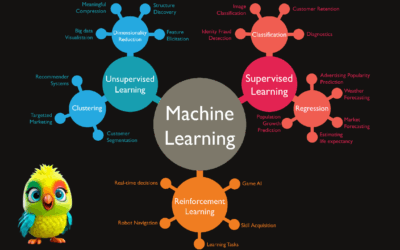
Every Model in Machine Learning (Supervised, Unsupervised, Regression) explained
What is artificial intelligence? Artificial intelligence is a field of science concerned with building computers and machines that can reason, learn, and act in such a way that would normally require human intelligence or that involves data whose scale exceeds what humans can analyze. AI is a large field that includes many disciplines including computer…
Terminal Commands: Dive Deep into the Power of Your Terminal
For many beginners, the terminal—or command-line interface (CLI)—can look intimidating: a blinking cursor, black background, and cryptic text. But once you unlock its power, the terminal becomes your best friend, especially for developers, sysadmins, and anyone managing servers or code. In this blog, we’ll explore terminal commands from beginner to advanced, focusing on their practical…
How to Automate Sending Sweet WhatsApp Messages to Your Partner Every Day
Being in love comes with a desire to stay connected—even when you’re busy. Whether it’s a warm “Good Morning” at 5:00 AM, a thoughtful midday check-in, or a sweet “Good Night,” consistent communication keeps the spark alive. But what if you could automate those loving messages without manually sending them every single day? In this…