What is Bias-Variance Trade-Off?
In the world of machine learning, the bias-variance trade-off is one of the most crucial concepts for building a successful model. It represents the delicate balance between two types of errors that can influence the performance of a model: bias and variance. These two sources of error can be thought of as opposing forces—when you reduce one, the other tends to increase. Understanding how they interact can help you build models that generalize well to unseen data.
To make good predictions, it’s important to strike the right balance between bias and variance. But how exactly do bias and variance work, and what does the trade-off mean?
Bias: The Simplification Error
Bias refers to the error introduced by simplifying a model too much. In other words, it’s the difference between the model’s predictions and the actual values due to the model’s assumptions or oversimplifications. High bias typically leads to underfitting, where the model is too simple to capture the complexity of the data, resulting in poor predictive performance.
Examples of Bias:
- Low-bias algorithms: These models can capture more complex patterns in the data. Examples include Decision Trees, K-Nearest Neighbors (k-NN), and Support Vector Machines (SVM).
- High-bias algorithms: These models make strong assumptions about the data and typically fail to capture important patterns. Examples include Linear Regression and Logistic Regression.
Variance: The Complexity Error
Variance refers to the model’s sensitivity to small fluctuations in the training data. A model with high variance performs well on the training set, but it overfits the data and struggles to generalize to new, unseen data. This is known as overfitting. High variance usually occurs in complex models that fit the training data too closely, capturing noise or irrelevant patterns that are not generalizable.
Examples of Variance:
- High-variance models: Complex models such as Polynomial Regression can exhibit high variance, especially if the degree of the polynomial is too high for the amount of training data.
- Low-variance models: Simpler models such as Linear Regression have low variance and tend to generalize well, although they may suffer from higher bias.
The Bias-Variance Trade-Off
As you increase the complexity of your machine learning model (e.g., by adding more features or using more complex algorithms), the bias tends to decrease (the model fits the data better), but the variance tends to increase (the model starts overfitting the data). This trade-off is a fundamental concept in machine learning, and your goal is to find the sweet spot where the bias and variance are balanced, resulting in a model that generalizes well.
Key Insights into Bias-Variance Trade-Off:
- Low bias, high variance: A model like k-NN (K-Nearest Neighbors) has low bias and high variance. It makes very few assumptions about the data but can be very sensitive to fluctuations in the training set. Increasing the value of k (the number of neighbors considered) can increase bias but reduce variance, as the model becomes less sensitive to individual data points.
- Low bias, high variance: A Support Vector Machine (SVM) with a small C parameter will have low bias and high variance. By increasing C, the model allows more violations of the margin (i.e., fewer misclassifications), which increases bias but reduces variance.
- High bias, low variance: Linear Regression typically exhibits high bias and low variance, meaning it simplifies the data relationships too much. Using more features or trying other regression methods can help reduce bias.
- Overfitting and Underfitting: Overfitting occurs when your model has high variance and performs poorly on unseen data. Underfitting happens when your model has high bias and is too simplistic to capture the data patterns.
How to Manage the Bias-Variance Trade-Off?
When building machine learning models, your objective is to minimize total error. Total error consists of three parts: bias error, variance error, and irreducible error (which is the noise inherent in the data). A model that has both low bias and low variance will achieve better predictive performance.
Here are some strategies to manage the bias-variance trade-off:
- Simplify the model: If your model has high variance, consider simplifying it by reducing its complexity. For example, decrease the depth of decision trees or reduce the number of polynomial features in regression models.
- Increase the data size: More data can help to reduce variance, as a larger sample can better represent the underlying distribution of the population.
- Regularization: Regularization techniques like L1 and L2 regularization can help reduce variance by penalizing overly complex models and forcing them to generalize better.
- Cross-validation: Use cross-validation to test how well your model generalizes to unseen data, which can help you spot overfitting or underfitting early.
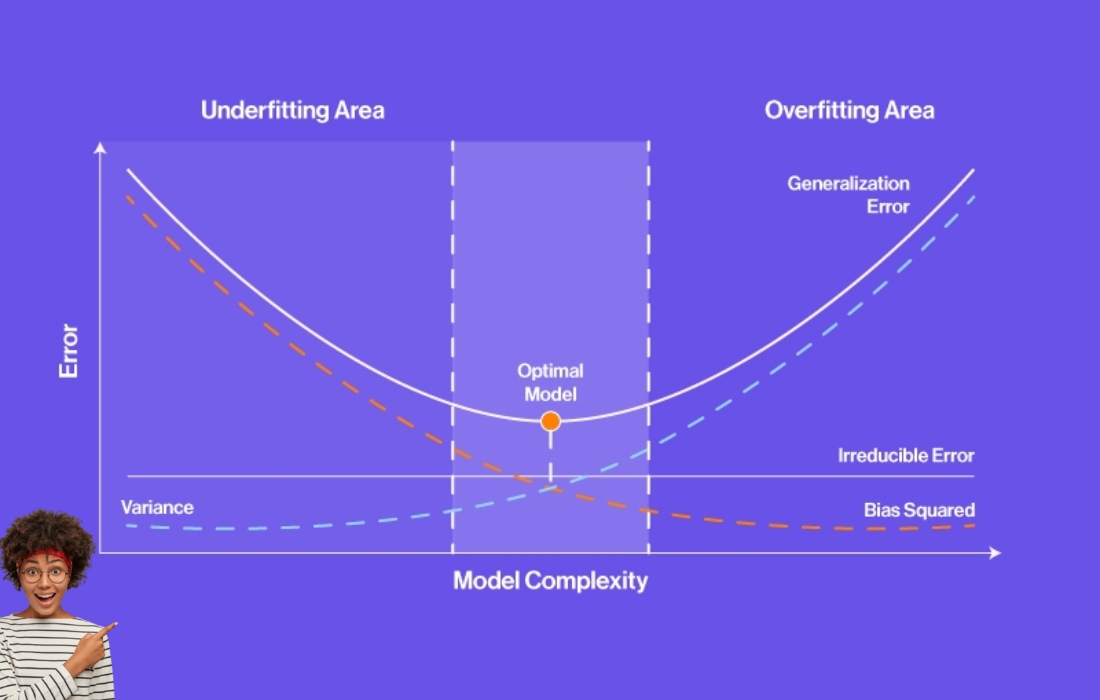
Visualizing the Bias-Variance Trade-Off
In a graphical representation of the bias-variance trade-off, we can see that:
- As model complexity increases (moving along the x-axis), bias decreases and variance increases.
- The total error (combination of bias and variance) reaches its minimum at the point where bias and variance balance each other out.
Image Description: The curve shows that as the complexity of the model increases, the bias decreases while the variance increases. The total error curve, which represents the sum of bias and variance, reaches its minimum at an optimal point of complexity.
Conclusion
The bias-variance trade-off is central to creating effective machine learning models. The key to success is understanding that both bias and variance contribute to the overall error in your model. Striving for low bias and low variance will lead to the best predictive performance. Achieving this balance is often an iterative process, and depending on the data and the algorithm, adjustments like increasing or decreasing model complexity, using regularization, or leveraging more data may be needed to optimize performance.
By mastering the bias-variance trade-off, data scientists and machine learning practitioners can design models that generalize well, providing accurate predictions while avoiding common pitfalls like overfitting and underfitting.
This blog is designed to clarify the importance of understanding and managing the bias-variance trade-off when building machine learning models. Properly addressing this trade-off will significantly improve the accuracy and robustness of your predictive models.