The Drama of the Cubic Equation: Rivalries, Betrayals, and Renaissance Mathematics
The 16th century was a time of mathematical duels, secret solutions, and bitter rivalries. The quest to solve the cubic equation wasn’t just about algebra—it was about fame, survival, and revenge.
1. Tartaglia: The Stuttering Genius Who Outsmarted His Rivals
Niccolò Tartaglia (1500–1557) was a self-taught mathematician who overcame a speech impediment (his nickname “Tartaglia” means “stammerer”). As a child, he survived a sword attack during the Sack of Brescia (1512), which left him with a lifelong stutter.
Despite his hardships, he became a brilliant mathematician. In 1535, he was challenged to a public math duel by Antonio Fiore, a student of Scipione del Ferro.
The Duel That Changed Mathematics
– Fiore had inherited del Ferro’s secret solution to the depressed cubic \( x^3 + p x = q \).
– Tartaglia, unaware of del Ferro’s work, had independently solved it.
– The duel consisted of 30 problems – each man gave the other a set of equations to solve.
– Tartaglia destroyed Fiore, solving all of Fiore’s cubics while Fiore failed to solve Tartaglia’s non-cubic problems.
This victory made Tartaglia famous – but also made him a target.
2. Cardano: The Gambler, Astrologer, and Mathematical Thief?
Gerolamo Cardano (1501–1576) was a polymath, physician, and compulsive gambler who wrote one of the first books on probability. He was also obsessed with solving the cubic.
How Cardano Tricked Tartaglia
– In 1539, Cardano begged Tartaglia for the cubic solution.
– Tartaglia reluctantly agreed -but only after Cardano swore an oath of secrecy.
– Tartaglia gave him the solution in cipher form (a poem with hidden mathematical steps).
But then…
The Betrayal
– Cardano discovered that del Ferro had solved the cubic first.
– He argued that this voided his oath to Tartaglia.
– In 1545, he published the solution in his book “Ars Magna” -giving credit to both del Ferro and Tartaglia, but breaking his promise.
Tartaglia was furious.
3. Ferrari: The Hot-Headed Protégé Who Crushed Tartaglia
Ludovico Ferrari (1522–1565) was Cardano’s student and bodyguard. He had a fiery temper and was fiercely loyal to Cardano.
The Public Humiliation of Tartaglia
– Tartaglia challenged Cardano to a debate in 1548.
– Instead of Cardano, Ferrari showed up – and destroyed Tartaglia mathematically.
– Ferrari solved every problem Tartaglia posed, while Tartaglia struggled.
– The audience mocked Tartaglia, and he left in disgrace.
Ferrari went on to solve the quartic equation (degree 4), which Cardano included in Ars Magna.
4. Life as a Mathematician in the Renaissance
– No universities paid for math research –mathematicians relied on patrons.
– Math duels were public spectacles, with wagered money and pride.
– Secrecy was key –solutions were hidden in poems or ciphers to avoid theft.
– Plagiarism was rampant -many discoveries were stolen or independently rediscovered.
5. The Ultimate Goal: Solving \( x^n = k \) (General Polynomial Equations)
The cubic and quartic solutions led to the question:
Can we solve \( x^n = k \) for any \( n \)?
– Quadratic: Solved by Babylonians (~2000 BC)
– Cubic: Solved by del Ferro/Tartaglia/Cardano (16th century)
– Quartic: Solved by Ferrari (1540)
– Quintic (n=5): Proven impossible by Abel & Galois (19th century)
Why Can’t We Solve the Quintic?
Galois proved that polynomials of degree 5+ cannot be solved by radicals (using only +, −, ×, ÷, and roots). Instead, they require elliptic functions or numerical methods.
Final Challenge: Solve a Cubic Like Tartaglia!
Problem: Solve \( x^3 + 6x = 20 \) using Cardano’s formula.
Solution:
1. Recognize it’s in depressed form \( x^3 + p x = q \) where \( p = 6 \), \( q = 20 \).
2. Compute discriminant:
\[
\Delta = \left( \frac{q}{2} \right)^2 + \left( \frac{p}{3} \right)^3 = 100 + 8 = 108
\]
3. Apply Cardano’s formula:
\[
x = \sqrt[3]{10 + \sqrt{108}} – \sqrt[3]{-10 + \sqrt{108}}
\]
4. Simplify:
\[
\sqrt{108} = 6 \sqrt{3}, \quad \sqrt[3]{10 + 6 \sqrt{3}} – \sqrt[3]{-10 + 6 \sqrt{3}} = 2
\]
(Check: \( 2^3 + 6 \times 2 = 8 + 12 = 20 \))
Answer: \( x = 2 \).
Complete Derivation of Cubic Solution & Extension to Higher-Degree Equations
Part 1: Solving the Cubic Equation (Step-by-Step Derivation)
Step 1: Depress the Cubic (Eliminate \(x^2\) Term)
Start with general cubic:
\[
x^3 + a x^2 + b x + c = 0
\]
Substitute \(x = y – \frac{a}{3}\):
\[
\left(y – \frac{a}{3}\right)^3 + a\left(y – \frac{a}{3}\right)^2 + b\left(y – \frac{a}{3}\right) + c = 0
\]
Expanding and simplifying, the \(y^2\) term cancels out:
\[
y^3 + \underbrace{\left(b – \frac{a^2}{3}\right)}_{p} y + \underbrace{\left(c – \frac{a b}{3} + \frac{2 a^3}{27}\right)}_{q} = 0
\]
Now in depressed form:
\[
y^3 + p y = q
\]
Step 2: Assume a Solution of the Form \(y = \sqrt[3]{u} – \sqrt[3]{v}\)
Cubing both sides:
\[
y^3 = u – v – 3 \sqrt[3]{u v} (\sqrt[3]{u} – \sqrt[3]{v}) = u – v – 3 \sqrt[3]{u v} y
\]
Substitute into depressed cubic:
\[
(u – v) – 3 \sqrt[3]{u v} y + p y = q
\]
For equality, set:
1. \(u – v = q\)
2. \(-3 \sqrt[3]{u v} + p = 0 \implies u v = \left(\frac{p}{3}\right)^3\)
Step 3: Solve for \(u\) and \(v\)
From \(u – v = q\) and \(u v = \left(\frac{p}{3}\right)^3\), we get a quadratic:
\[
u^2 – q u – \left(\frac{p}{3}\right)^3 = 0
\]
Solutions:
\[
u = \frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}, \quad v = – \frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}
\]
Final solution (Cardano’s Formula):
\[
y = \sqrt[3]{\frac{q}{2} + \sqrt{D}} – \sqrt[3]{-\frac{q}{2} + \sqrt{D}}, \quad \text{where } D = \left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3
\]
Revert substitution \(x = y – \frac{a}{3}\) for original cubic.
Part 2: Solving Quartic (4th Degree) Equations (Ferrari’s Method)
Step 1: Depress the Quartic (Remove \(x^3\) Term)
Start with:
\[
x^4 + a x^3 + b x^2 + c x + d = 0
\]
Substitute \(x = y – \frac{a}{4}\) to eliminate \(x^3\):
\[
y^4 + P y^2 + Q y + R = 0
\]
Step 2: Introduce an Auxiliary Cubic
Rewrite as:
\[
y^4 = -P y^2 – Q y – R
\]
Add \(2 z y^2 + z^2\) to both sides:
\[
y^4 + 2 z y^2 + z^2 = (2 z – P) y^2 – Q y + (z^2 – R)
\]
Left side is \((y^2 + z)^2\). To make right side a perfect square:
\[
\text{Discriminant} = Q^2 – 4 (2 z – P)(z^2 – R) = 0
\]
This gives the resolvent cubic:
\[
z^3 – \frac{P}{2} z^2 – R z + \frac{4 P R – Q^2}{8} = 0
\]
Solve for \(z\) using Cardano’s method, then take square roots.
Part 3: The Quintic (5th Degree) and Beyond
Why Quintics Can’t Be Solved by Radicals
– Abel-Ruffini Theorem (1824): No general algebraic solution exists for quintics (\(x^5 + \dots = 0\)) using radicals (+, −, ×, ÷, roots).
– Galois Theory: Proves that polynomials of degree \(n \geq 5\) have symmetry groups too complex for radical solutions.
Numerical Methods for Higher-Degree Equations
For \(x^n + \dots = 0\) where \(n \geq 5\):
1. Newton-Raphson Method: Iterative approximation.
2. Factorization: If possible, reduce to lower-degree factors.
3. Elliptic Functions: Required for some quintic forms.
Solved Examples
Example 1: Cubic Equation
Solve \(x^3 – 6 x^2 + 11 x – 6 = 0\).
1. Depress: Substitute \(x = y + 2\) → \(y^3 – y = 0\).
2. Solutions: \(y = 0, \pm 1\) → \(x = 1, 2, 3\).
Example 2: Quartic Equation
Solve \(x^4 – 3 x^2 + 2 = 0\).
1. Let \(z = x^2\) → \(z^2 – 3 z + 2 = 0\).
2. Solutions: \(z = 1, 2\) → \(x = \pm 1, \pm \sqrt{2}\).
Example 3: Quintic (Numerical Approach)
Solve \(x^5 – x – 1 = 0\).
– Newton’s method: Start with \(x_0 = 1\) → \(x_{n+1} = x_n – \frac{x_n^5 – x_n – 1}{5 x_n^4 – 1}\).
– Converges to \(x \approx 1.1673\).
Key Takeaways
1. Cubics: Solved via substitution and Cardano’s formula.
2. Quartics: Reduced to cubics using Ferrari’s method.
3. Quintics+: No general radical solution; use numerical methods.
For \(x^n\) equations:
– \(n \leq 4\): Algebraic solutions exist.
– \(n \geq 5\): Require advanced methods.
Conclusion
The cubic equation’s history is a tale of genius, rivalry, and betrayal –but also the birth of modern algebra. While we can’t solve all equations with radicals, the quest led to group theory, complex numbers, and deeper math.



















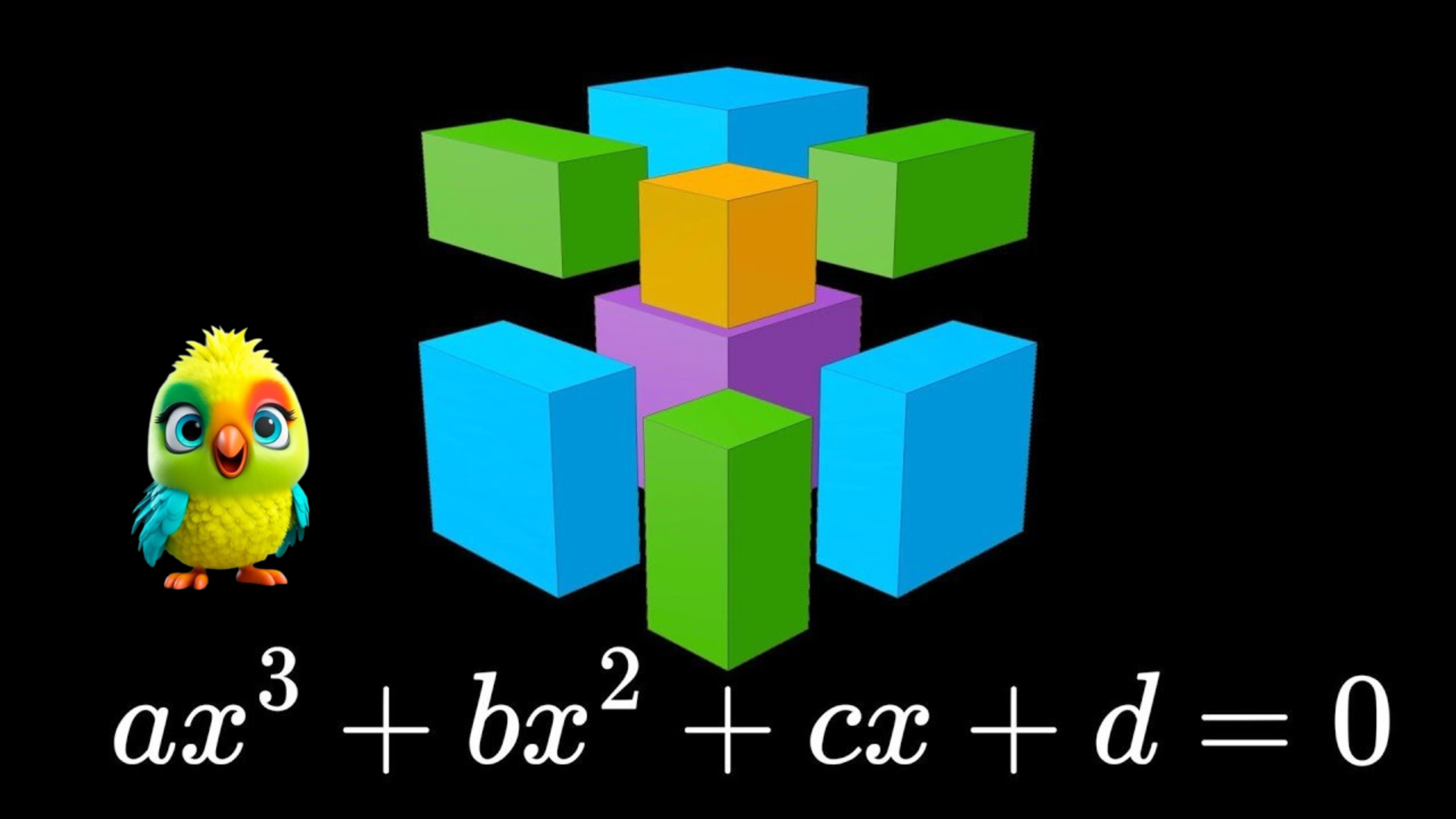
I like your content a lot… ♥️