Education
Expand Your Knowledge with Our Education Courses: Learn, Grow, and Succeed
Discover a wide array of education-focused courses designed to enhance your academic and professional growth. From early childhood education to advanced teaching techniques, our courses cater to educators, parents, and anyone passionate about learning. Gain valuable skills in curriculum development, classroom management, educational technology, and more. Whether you’re looking to become a teacher, advance your career in education, or simply deepen your understanding, our courses offer the tools you need to succeed and inspire others.
The Epic Saga of the Cubic Equation: From Blood Feuds to Modern Algebra
The Drama of the Cubic Equation: Rivalries, Betrayals, and Renaissance Mathematics The 16th century was a time of mathematical duels, secret solutions, and bitter rivalries. The quest to solve the cubic equation wasn’t just about algebra—it was about fame, survival, and revenge. 1. Tartaglia: The Stuttering Genius Who Outsmarted His Rivals Niccolò Tartaglia (1500–1557) was…
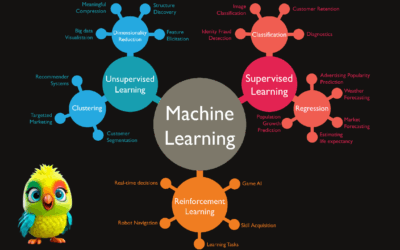
Every Model in Machine Learning (Supervised, Unsupervised, Regression) explained
What is artificial intelligence? Artificial intelligence is a field of science concerned with building computers and machines that can reason, learn, and act in such a way that would normally require human intelligence or that involves data whose scale exceeds what humans can analyze. AI is a large field that includes many disciplines including computer…
Terminal Commands: Dive Deep into the Power of Your Terminal
For many beginners, the terminal—or command-line interface (CLI)—can look intimidating: a blinking cursor, black background, and cryptic text. But once you unlock its power, the terminal becomes your best friend, especially for developers, sysadmins, and anyone managing servers or code. In this blog, we’ll explore terminal commands from beginner to advanced, focusing on their practical…
How to Automate Sending Sweet WhatsApp Messages to Your Partner Every Day
Being in love comes with a desire to stay connected—even when you’re busy. Whether it’s a warm “Good Morning” at 5:00 AM, a thoughtful midday check-in, or a sweet “Good Night,” consistent communication keeps the spark alive. But what if you could automate those loving messages without manually sending them every single day? In this…
What Are Numbers, Really? A Gentle Dive into Number Theory, Mathematics with Python
Numbers are everywhere. From managing finances to analyzing data, we constantly interact with them. But what exactly are numbers? In this post, we’ll explore the beautiful journey of numbers through number theory, and bring it all together with a Python program that showcases each type of number in action. The Evolution of Numbers Natural Numbers…
Understanding the Difference Between Long and Wide Format Data in Data Analysis
What is the Difference Between Long and Wide Format Data? In data analysis and data science, organizing your data correctly is a crucial step that can significantly impact the efficiency and accuracy of your analysis. Two common ways to organize data are long format and wide format. Understanding the difference between the two formats…
Mastering Android Development with Kotlin & Android Studio
This course is designed for beginners and intermediate developers interested in learning how to build Android applications using Kotlin and Android Studio. By the end of the course, you’ll have hands-on experience with Android Studio, Kotlin programming, and essential Android development tools and techniques.
An Overview of Mathematics in Classical Mechanics
Classical mechanics, developed primarily through the work of Sir Isaac Newton and subsequent physicists such as Euler, Lagrange, and Hamilton, provides the foundation for understanding the motion of physical systems under the influence of forces.
Derivation and Examples of Reduction Formulas
In this section, we will derive and provide examples for various reduction formulas used in calculus. Each formula allows us to reduce the complexity of integrals involving different types of functions, such as exponential, trigonometric, inverse trigonometric, hyperbolic, logarithmic, and algebraic functions.
A Comprehensive Guide to Series in Real Analysis
In real analysis, series play an important role in understanding the convergence properties of sequences and functions. A series is essentially the sum of the terms of a sequence, and the study of series provides the foundation for advanced concepts such as Taylor series, Fourier series, and more.